UCSNet

基本信息

项目 内容
论文标题 UCSNet (Uncertainty-aware Cascaded Stereo Network)
作者 Shuo Cheng, Zexiang Xu, Shilin Zhu, Zhuwen Li, Li Erran Li, Ravi Ramamoorthi, Hao Su
作者单位 University of California San Diego
时间 2020
发表会议/期刊

方法概览

特点 文章性质
输入 多视角
输出 参考视角深度图
所属领域 MVS

1. 摘要精简

提出一种不确定性感知的级联立体匹配网络 UCS-Net，用于多视图图像的 3D 重建。该方法摒弃传统固定深度假设的代价体，提出自适应薄体积（ATV），其深度假设随空间位置变化，适配前一阶段的像素级深度预测不确定性。UCS-Net 包含三阶段级联架构：第一阶段用小型标准平面扫描代价体预测低分辨率深度；后两阶段通过 ATV 逐步细化，以更高分辨率和精度优化深度。ATV 仅含少量深度平面，但通过学习到的局部深度区间实现高效空间划分，结合可微分的方差基不确定性估计，实现粗到精的高质量重建，在多个基准数据集上性能超越 SOTA，兼顾精度与完整性。

2. 研究出发点

现有学习型 MVS 方法的核心瓶颈是 “精度 - 完整性 - 内存” 的权衡：传统平面扫描代价体依赖固定深度假设，需密集采样深度平面才能保证精度，导致内存消耗巨大，难以实现高分辨率深度重建；而稀疏采样虽降低内存，却会损失完整性。此外，现有方法未利用深度预测的不确定性信息，无法自适应调整深度采样范围。因此，本文旨在通过 “不确定性感知的自适应采样 + 多阶段粗到精框架”，打破上述权衡，在中等内存消耗下同时实现高精度与高完整性。

3. 创新点

  • 提出自适应薄体积（ATV）：深度假设随空间位置变化，围绕前一阶段的深度预测及不确定性区间构建，仅需少量平面即可实现细粒度局部深度划分，大幅提升采样效率；
  • 设计可微分方差基不确定性估计：利用前一阶段深度概率分布的方差计算置信区间，指导 ATV 的深度采样，确保采样范围覆盖真值且足够紧凑，该过程可微分，支持端到端训练；
  • 构建三阶段级联粗到精框架：从低分辨率粗深度逐步优化至原始图像分辨率，每阶段适配对应尺度的特征与代价体，兼顾效率与重建质量；
  • 各阶段采用独立 3D U-Net处理代价体，不共享权重，确保每个阶段能针对性学习对应尺度的几何信息。

4. 网络架构

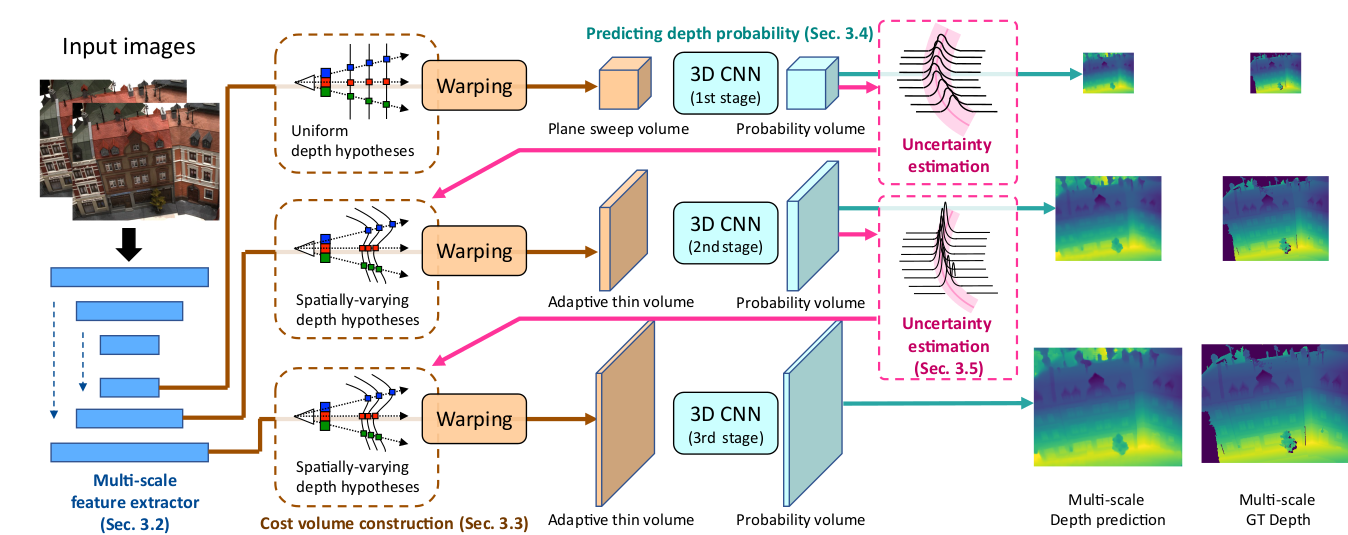
image-20251126230733925

网络整体为三阶段级联结构，流程为 “多尺度特征提取→分阶段代价体构建→3D CNN 正则化→深度预测→不确定性估计→ATV 构建→迭代细化”：

  1. 多尺度特征提取：2D U-Net 生成三个尺度的图像特征，为后续分阶段代价体提供输入；
  2. 第一阶段：基于低分辨率特征构建标准平面扫描代价体（160 个均匀采样深度平面），3D U-Net 正则化后输出低分辨率深度图与概率体积；
  3. 第二 / 三阶段：基于前一阶段的深度预测与不确定性估计，构建 ATV（分别含 16/8 个深度平面），对应中 / 高分辨率特征，经 3D U-Net 正则化后输出更高分辨率的深度图；
  4. 后处理：多视图深度图融合为 3D 点云，采用传统融合策略保证一致性。

三阶段级联网络：

  • 第一阶段：标准平面扫描体积，低分辨率（160个深度平面）
  • 第二阶段：自适应薄体积，中等分辨率（16个深度平面）
  • 第三阶段：自适应薄体积，高分辨率（8个深度平面）

5. 特征提取

使用2D U-Net作为多尺度特征提取器：

  • 网络结构：含编码器（两次步长为 2 的下采样）与解码器（两次上采样），带跳接连接，每层卷积后接分组归一化（GN）与 ReLU 激活；
  • 输出三个尺度的特征图：W4×H4×32\frac{W}{4}×\frac{H}{4}×32、W2×H2×16\frac{W}{2}×\frac{H}{2}×16、W×H×8W×H×8
  • 通过学习的上采样过程将低分辨率信息整合到高分辨率特征中

6. 代价体构建

第一阶段：标准平面扫描体积

  • 均匀采样 160 个固定深度值,深度假设：L1,j(x)=dj\mathbf{L}_{1,j}(x)=d_j
  • 使用单应性变换Hi(d)=Ki[Ri,ti]−1[R1,t1]K1\mathbf{H}_i(d)=K_i[R_i,t_i]^{-1}[R_1,t_1]K_1扭曲特征

第二、三阶段：自适应薄体积ATV

  • 首先计算前一阶段深度预测的概率分布方差：

V^k(x)=∑j=1DkPk,j(x)⋅(Lk,j(x)−L^k(x))2\hat{\mathbf{V}}_k(x) = \sum_{j=1}^{D_k} \mathbf{P}_{k,j}(x) \cdot (\mathbf{L}_{k,j}(x) - \hat{\mathbf{L}}_k(x))^2

其中：

V^k(x)\hat{\mathbf{V}}_k(x)：像素x在阶段k的深度方差

Pk,j(x)\mathbf{P}_{k,j}(x)：深度假设Lk,j(x)\mathbf{L}_{k,j}(x)的概率

L^k(x)\hat{\mathbf{L}}_k(x)：期望深度值

标准差计算：

σ^k(x)=V^k(x)\hat{\sigma}_k(x) = \sqrt{\hat{\mathbf{V}}_k(x)}

  • 然后计算置信区间构建

基于方差计算每个像素的深度置信区间：

Ck(x)=[L^k(x)−λσ^k(x),L^k(x)+λσ^k(x)]\mathbf{C}_k(x) = [\hat{\mathbf{L}}_k(x) - \lambda\hat{\sigma}_k(x), \hat{\mathbf{L}}_k(x) + \lambda\hat{\sigma}_k(x)]

其中λ\lambda是控制区间大小的标量参数（论文中使用λ=1.5\lambda=1.5）。

  • 最后自适应深度采样

对于每个像素x，在其置信区间Ck(x)\mathbf{C}_k(x)内均匀采样Dk+1D_{k+1}个深度值：

Lk+1,1(x),Lk+1,2(x),…,Lk+1,Dk+1(x)\mathbf{L}_{k+1,1}(x), \mathbf{L}_{k+1,2}(x), \ldots, \mathbf{L}_{k+1,D_{k+1}}(x)

7. 代价体正则化

每个阶段的代价体独立采用 3D U-Net 进行正则化，网络结构一致但不共享权重：3D U-Net 架构：含两次下采样（步长 2）与两次上采样（步长 2），带跳接连接，每层卷积（除最后一层）后接批归一化（BN）与 ReLU 激活；

  • 在深度维度应用softmax预测深度概率分布
  • 三个阶段使用相同架构但不共享权重

8. 深度图生成

从深度概率分布计算期望值：

L^k(x)=∑j=1DkLk,j(x)⋅Pk,j(x)\hat{\mathbf{L}}_k(x)=\sum_{j=1}^{D_k}\mathbf{L}_{k,j}(x)\cdot\mathbf{P}_{k,j}(x)

10. 损失函数

使用L1损失：

  • 在三个分辨率上分别计算深度预测与真值的L1损失
  • 最终损失为三个损失的加权和

11. 训练策略

  • 先单独训练第一阶段10个epoch
  • 然后端到端训练全部三个阶段20个epoch
  • 使用Adam优化器，初始学习率0.001

12. 测试数据集

  • DTU数据集：室内场景，用于主要评估

  • Tanks and Temple数据集：室外复杂场景，用于泛化能力测试