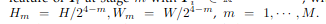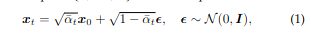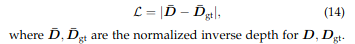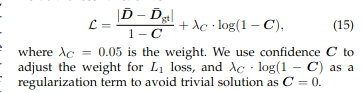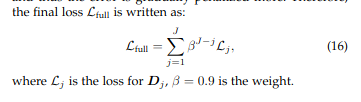基本信息

项目	内容
论文标题	Lightweight and Accurate Multi-View Stereo with Confidence-Aware Diffusion Model
作者	Fangjinhua Wang（patchmatchNet作者，IterMVS）, Qingshan Xu（ACMH作者）, Yew-Soon Ong
作者单位	ETH
时间	20250906
发表会议/期刊	TiPami

方法概览

特点	文章性质
输入	标定之后的多视角图像
输出	场景的点云图
所属领域	MVS

背景

创新点

首个将Diffusion引入到MVS的工作

网络架构

构建一个图像集。（与视觉 SLAM 中常见的做法类似）我们将一张图像设为关键帧，当其与上一帧关键帧之间的视差（我们使用 Lucas-Kanade 方法估计）大于用户设定的阈值时就作为一个新的关键帧。并被添加到图像集。直到该图像集的大小达到设定的上限。然后维护多个图像集。多个图像集的前后帧是重叠帧
然后这多个图像集分别传入VGGT生成局部子图

摘要

将深度细化表述为一个条件扩散过程。考虑到深度估计的判别特性，我们设计了一个条件编码器来指导扩散过程。为了提高效率，我们提出了一种结合轻量级二维 U-Net 和卷积 GRU 的新型扩散网络。此外，我们提出了一种新的基于置信度的抽样策略，以基于扩散模型估计的置信度对深度假设进行自适应采样。基于我们新颖的 MVS 框架，我们提出了两种新的 MVS 方法，DiffMVS 和 CasDiffMVS。DiffMVS 在运行时和 GPU 内存方面以最先进的效率实现了具有竞争力的性能。CasDiffMVS 在 DTU、Tanks & Temples 和 ETH3D 上实现了最先进的性能。

引言

**MVS 本质上是具有光度一致性假设的有限连续深度空间中的最优对应搜索问题。**然而，由于现实场景中常见的照明变化、非朗伯表面和低纹理区域的干扰，准确估计深度具有挑战性。
从粗到细的方法初始化了深度范围内稀疏样本的低分辨率深度图，逐渐以更高的分辨率对其进行细化，并减少更精细的深度范围，在很大程度上依赖于粗深度图的质量，在这项工作中，我们重新思考如何通过不仅以先前的粗略估计为条件，而且通过引入随机扰动来执行准确的多视图深度估计。最近，扩散模型表明，注入随机噪声可以避免坍缩为局部最小值。受扩散模型的启发，该模型可以通过迭代去噪过程从随机噪声中恢复数据样本，我们希望我们的多视图深度估计能够模拟去噪过程，引入随机噪声并产生准确的估计。
然而，由于多视图深度估计是判别感知任务 discriminative perception task，而不是无条件生成任务unconditional generative task，在多视图深度估计中引入基于扩散的去噪过程将面临以下挑战：
1. Diffusion conditions.：为了获得准确的确定性估计，重要的是要根据一些特定的指导来调节扩散网络。由于匹配信息对于 MVS 中获得准确的深度估计至关重要，因此自然需要引入匹配信息作为扩散条件。然而，MVS 是否需要其他扩散条件，或者如何将匹配信息整合到扩散模型中，目前还没有得到充分的探索。
2. Diffusion sampling：对于生成任务，扩散模型常仅使用该样本的信息对噪声样本进行降噪。对于判别性任务，如特征匹配，使用单个样本的信息只能提供零阶优化信息，这使得它无法利用非局部信息进行更准确的一阶优化。这阻碍了对扩散模型判别感知任务的准确估计？
3. Diffusion efficiency：堆叠 U-Net 有利于提高性能。然而，这些设计将不可避免地阻碍效率
提出了两种新颖的 MVS 方法，分别称为 DiffMVS 和 CasDiffMVS。DiffMVS 使用单级扩散模型进行深度细化，而 CasDiffMVS 扩展 DiffMVS 并在两个阶段进行深度细化。前者专为实时应用量身定制，而后者专为高精度要求而设计。DiffMVS 在运行时和内存方面SOTA，而 CasDiffMVS 在各种基准测试上以高效率实现了 SOTA 重建性能，综上所述，我们的贡献如下：
1. 我们提出了一种新型的 MVS 框架，该框架利用条件扩散模型来实现高效、准确和轻量级的多视图深度估计。
2. 提出了一种条件编码器，将匹配信息、图像上下文和深度上下文特征融合在一起，作为扩散模型的条件输入。这为生成准确的深度预测提供了扩散模型特定的指导。
3. 我们引入了一种基于置信度的抽样策略，该策略自适应地在基于扩散模型估计的置信度的局部范围，提供信息丰富的一阶优化方向。我们的采样基于受扩散过程中的随机噪声扰动的噪声粗略估计。这引入了随机性，但如果我们在固定范围内生成深度假设[19]，[22]，则可能缺乏信息丰富的一阶优化信息，因为粗略估计可能会受到随机噪声的很大干扰。为了解决这个问题，我们基于置信度的采样策略利用每像素预测置信度来自适应调整采样范围并捕获非局部一阶优化信息，从而促进去噪过程？
4. 我们开发了一个轻量级扩散网络，它利用卷积 GRU 来取代经典扩散模型中使用的大型去噪 U-Net。
5. 基于我们新颖的 MVS 框架，我们提出了两种新的 MVS 方法，DiffMVS 和 CasDiffMVS。前者在运行时和内存方面都实现了具有 SOTA 效率的竞争性能，而后者则在各种基准测试中实现了 SOTA 性能。

方法

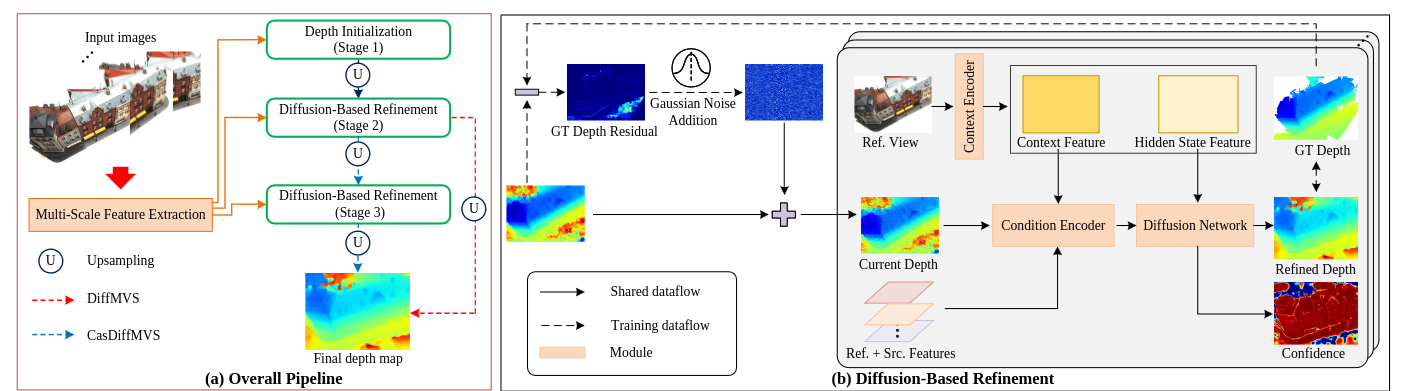
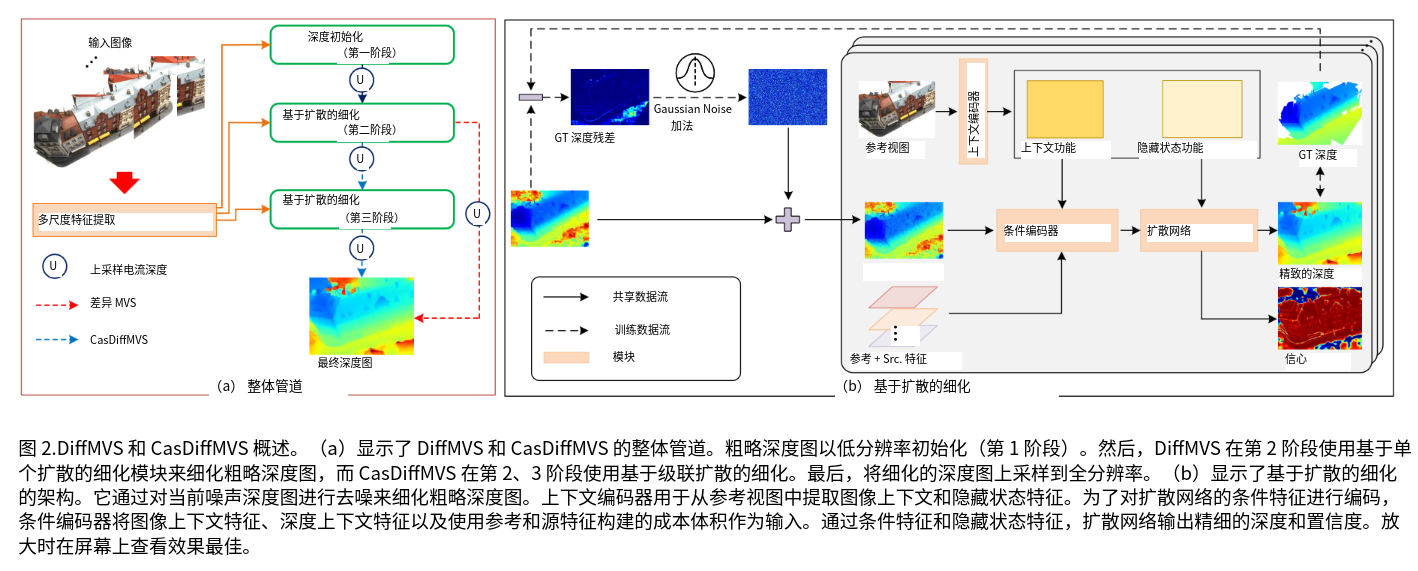
由两个模块组成：深度初始化和基于扩散的深度细化。从结构上讲，DiffMVS 在单个阶段（第 2 阶段）上执行深度细化，然后上采样到全分辨率，而 CasDiffMVS 在两个阶段（第 2、3 阶段）执行细化，然后上采样到全分辨率。

Preliminaries

这里讲解了Diffusion基本内容

在推理阶段，基于扩散网络 f（·）和更新原理，以迭代方式从高斯噪声重建 x。为了获得良好的性能，DDPM需要对许多步骤进行采样，因此采样效率较低。相比之下，DDIM提出了非马尔可夫正向过程，该过程能够以更少的采样步骤生成高质量的样品。

Problem Formulation and Motivation（没看懂）

这里说了他们用diffusion的方法，是最大化后验深度图，之前的MVSNet都是用argmax这样的方法回归出深度图，一方面多尺度方法会卡再局部深度范围，另一方面会没有明确考虑先验log(D|Dinit)？

多尺度特征提取

使用特征金字塔网络（FPN）多尺度数目M：DiffMVS：M = 2，CasDiffMVS：M = 3。尺度如下
对于参考图像 I，我们进一步使用上下文 FPN 编码器提取多尺度上下文特征 F 和隐藏状态特征 h(tanh计算一下)，用于上采样和扩散模型。

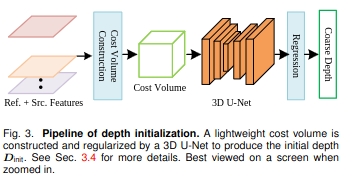
深度初始化(就是用了逆深度和组相关的MVSNet)

在第 1 阶段初始化粗略深度图（1/8 分辨率），然后使用扩散模型以更高的分辨率对其进行细化。
给定预定义的深度范围 [d， d]，我们在逆范围 [1/d， 1/d] 中均匀采样每像素深度。逆采样被认为更适合大规模场景
使用逐组相关来计算参考特征 F（p）和扭曲源特征 F（p）之间的相似性。将特征分成4组G=4，这样生成的代价体是H*W*D*G
用轻量级 3D U-Net 对 V 进行正则化，然后沿深度维度应用 softmax 以产生概率体积

与生成任务中的无条件扩散模型不同[23]，深度估计是一项判别感知任务，因此我们的扩散模型以条件编码器编码的特征为条件，因此可以约束生成多样性，从而可以准确地对深度图进行去噪。

**Forward process：**用逆深度归一化的深度来初始化扩散过程的深度图，预测这个D0和归一化逆深度的GT的差值X0。在训练过程中，我们对时间步长 t ∼ U （1， T ）进行均匀采样，并用式 1 计算噪声 x。

Reverse process.：

在之前的工作[23？]、[24？]之后，我们设计了基于 2D U-Net 架构的条件去噪扩散模型

最近，RAFT 在光流估计中很受欢迎，因为它使用 GRU 进行迭代细化，以低复杂性实现令人印象深刻的性能。在 RAFT 的推动下，许多stereo[84]/MVS[28]、[54]、[85]方法采用具有轻量级 2D 卷积的迭代 GRU 细化，以优于具有繁琐 3D 卷积的单一细化。由于我们在这项工作中同时关注效率和性能，将卷积 GRU 引入轻量级 2D U-Net。

在每个扩散时间步长t中，我们迭代细化 K 次。请注意，最近的扩散模型，例如 DiffusionDet [31]和 DifFlow3D [79]，也在每个扩散时间步长t’中更新了多次迭代k，以提高判别感知任务的性能。具体来说，在扩散时间步长 t 的第 k 次迭代中，我们的扩散模型预测了深度残差∆x 和置信度 Cof 电流估计的更新。K 次迭代后，深度残差被去噪为：

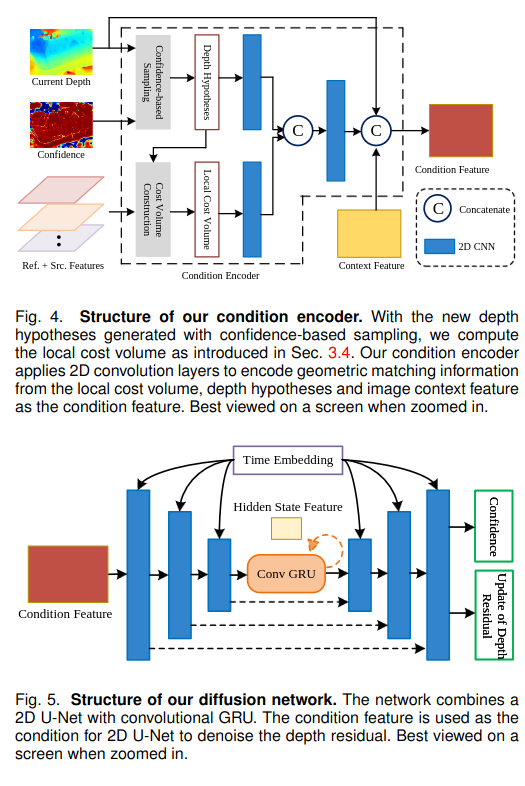
Condition encoder：

在第 k 次迭代中，我们首先在先前深度估计 ̄D 的局部范围内对像素新假设进行采样，从而得到 ̄Dk-1 ∈ R（后面将介绍具有置信度的采样策略的详细信息）。其次，我们计算新假设的局部成本体积 Lk∈ H*W*D*G，并将其进一步重塑为H*W*(D*G)。对于等式 7 中的视图权重 {W}i，我们重用了在第 1 阶段预测的视图权重，并使用最近邻对其进行上采样。

对于扩散模型，深度，代价体，深度图和图像之间的一致性有助于细化深度图。因此，我们提出了一种轻量级条件编码器，具体来说，是 2D 卷积层处理的成本体积 L。此外，我们在̄Dk 上应用二维卷积层来生成深度上下文特征。然后，我们将这两个特征连接起来，应用二维卷积层，最终与前面的深度 ̄D 和参考上下文特征 Fas 作为扩散模型的条件输入进行连接。

Denoising U-Net with GRU

继之前的工作[23Denoising diffusion probabilistic models]、[24High-resolution image synthesis with latent diffusion model就是sitable diffuison] 之后，我们设计了基于 2D U-Net 架构的条件扩散模型。在 DDPM [23]之后，我们将时间步长嵌入注入到 U-Net 的层中。我们通过实验发现，DDPM 中使用的注意力作并没有显性提高性能。因此，我们不会在 U-Net 中引入注意力，以便模型高效且轻量级。

如前所述，我们考虑到效率和性能，将 GRU 引入 2D U-Net。我们的扩散网络的结构如图 5 所示。具体来说，我们引入了 U-Net 最低分辨率的卷积 GRU(Conv GRU)。

要初始化 GRU 的隐藏状态：在参考图像的隐藏状态特征上应用二维卷积层，然后应用 tanh 非线性。

在第 k 次迭代中，U-Net 对条件编码器中的条件特征进行编码，将 GRU 的隐藏状态 h 更新。然后解码以预测深度残差∆x 的更新，以及当前深度估计的置信度 C（sigmoid 应用于置信度以确保 C∈[0,1]）。

Confidence-based sampling:

为了细化粗略的深度图，许多 MVS 方法[6]、[19]、[22]、[28]、[54]使用所有像素的恒定搜索范围来围绕先前的估计生成新的深度假设。

然而在抽样中使用置信度/不确定性是合理的。具体而言，对于估计准确的像素，应缩小搜索范围，以进一步提高准确率，而对于估计错误的像素，应扩大搜索范围，以便搜索范围覆盖地面实况。例如，UCSNet [20]计算了每个像素的采样范围，其中包含多个阶段的概率体积的方差。但是，这不适合我们的框架，因为我们在细化过程中不估计概率体积。

我们根据扩散模型的置信度 C 自适应调整每像素采样范围 R。对于第一次迭代 k = 1，我们将 R= R 设置为 R，其中 Ris 是每个阶段的预定义范围。对于 k > 1，Ris 计算为：

基于学习的上采样

我们没有使用简单的双线性或最近插值对不同阶段之间的深度进行上采样

而是使用带有掩码[27Raft]、[28Itermvs]的学习上采样，这通过实验提高了性能。具体来说，我们将上采样深度中每个像素的深度值计算为其粗分辨率邻居的 3 × 3 网格的凸组合（convex combination of a 3 × 3 grid）

对于阶段 m，我们通过在特征 F 上应用 2D 卷积层来预测形状为 H× W× （r × r × 9）的掩码，其中 r 是上采样率。然后，我们对 9 个邻居的权重应用 softmax，并将上采样深度预测为邻域的加权组合。

损失函数

损失函数 L 包括所有深度图的损失，即初始深度 D、基于扩散的细化 {D} 内的中间深度在时间步长 t 以及所有上采样的深度图。

对于深度图：按照 IterMVS [28]，我们将深度图 D 转换为公式 9 的归一化逆空间，并计算 Lloss 与地面实况深度图 D的归一化逆深度差值：

对于基于扩散的细化中的深度图 D：我们估计相应的置信度 C，我们将 C 包含在损失函数中，如下所示：

继[27]、[28]、[54]之后，我们对深度图使用指数递增的权重来平衡不同阶段和迭代之间的深度监督。动机是深度应该从粗到细估计，因此误差会逐渐受到更多惩罚。

实现

发现使用标准高斯噪声，即 N（0，I），如 DDPM [23]，将引入太强的噪声，无法进行细化。因此，我们将阶段 m 的高斯噪声设置为 N（0，σI）来控制噪声尺度。具体来说，当在 DTU 上训练时，我们将第 2 阶段的细化设置为 σ= 0.5，在第 3 阶段的细化设置为 σ= 0.1。

论文阅读_DiffMVS